Dans la conception habituelle de cadrans solaires, le Soleil projette l'ombre du style sur une surface plane marquée de lignes indiquant les heures de la journée. Comme le Soleil se déplace dans le ciel, la limite de l'ombre projetée s'aligne progressivement sur les différentes lignes horaires de la plaque. Dans cette conception de cadran, le style doit être aligné sur l'axe de rotation de la Terre.
Le style (une tige mince ou une pièce mince en forme de coin) doit être parallèle à l'axe de rotation de la Terre et doit pointer vers le pôle céleste. La surface sur laquelle l'ombre est projetée est appelée la 'face du cadran', ou plus simplement la 'face'.
Cadrans solaires verticaux
Dans le cas du 'cadran solaire vertical' de type commun, le plan sur lequel l'ombre est projetée est aligné verticalement. L'angle 'φ' du style avec la verticale doit être égal à la co-latitude qui vaut 90° moins la latitude géographique 'λ':
φ = 90° – λ
Cependant, la ligne d'ombre ne se dáplace pas uniformáment sur la face: le cadran solaire n'est pas áqui-angulaire. Si la face du cadran vertical pointe directement vers le Sud, l'angle des lignes horaires est alors dácrit par la formule:
tan(θ) = cos(λ) × tan(15° × t)
Dans cette formule, 'λ' est la latitude géographique du cadran solaire, 'θ' est l'angle entre une ligne horaire donnée et la ligne de midi (qui pointe toujours vers le Nord vrai) sur le plan, et 't' est le nombre d'heures avant ou après l'heure du midi solaire. Par exemple, l'angle θ de la ligne horaire des 3 heures de l'après-midi sera égal à l'arctangente de cos(λ), car tangente(45°) = 1. De façon intéressante, l'ombre se déplace dans le sens anti-horaire sur un cadran vertical faisant face au Sud alors qu'elle se déplace dans le sens horaire sur les cadrans horizontaux et équatoriaux.
Cadrans solaires horizontaux
Dans le cas du 'cadran solaire horizontal' de type commun, le plan sur lequel l'ombre est projetée est aligné horizontalement. L'angle du style avec le plan doit être égal à la latitude géographique du cadran solaire 'λ'.
Comme c'est aussi le cas pour le cadran solaire vertical, la ligne d'ombre ne se déplace pas uniformément sur le plan: le cadran solaire horizontal n'est pas non plus équi-angulaire. Si le style pointe directement vers le Nord vrai, l'angle des lignes horaires est décrit par la formule:
tan(θ) = sin(λ) × tan(15° × t)
Dans cette formule, 'λ' est la latitude géographique du cadran solaire, 'θ' est l'angle entre une ligne horaire donnée et la ligne horaire du midi solaire (qui pointe toujours vers le Nord vrai) sur le plan, et 't' est le nombre d'heures avant ou après midi. Par exemple, l'angle θ de la ligne horaire des 3 heures de l'après-midi sera égale à l'arctangente de sin(λ) car tangente(45°) = 1. De façon intéressante, l'ombre se déplace dans le sens horaire sur les cadrans horizontaux et équatoriaux alors qu'elle se déplace dans le sens anti-horaire sur un cadran vertical faisant face au Sud.
Notez que l'angle θ entre une ligne horaire donnée et la ligne horaire de midi n'est pas le même pour les cadrans verticaux et horizontaux.
Cadrans solaires combinés
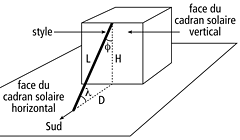
Un cadran solaire vertical et un cadran solaire horizontal peuvent être combinés en partageant le même style, car les angles du style sont complémentaires, c.a.d. de somme égale è 90°. Le plan du cadran solaire horizontal peut aussi être utilisé en tant que plaque support de cube. Dans ce cas, le style commun aux deux cadrans doit seulement être fixé sur le cadran horizontal et non pas sur le cube. La longueur 'L' du style commun et la distance 'D' de l'extrémité du style au cube sont données par:
L = H / sin(λ) et D = H / tan(λ)
Dans ces formules, 'λ' est la latitude géographique du cadran solaire et 'H' est la hauteur du cube, habituellement égale è 57 mm pour un Cube de Rubik ordinaire.
Le style peut être fabriqué è partir d'une tige en matière plastique de 3 mm de diamètre, qui doit être biseautée è ses deux extrémités. L'extrémité inférieure de la tige peut ensuite être collée sur la plaque support alors que son extrémité supérieure s'appuie librement sur le petit cube central de la rangée supérieure.
Corrections finales
Trois corrections sont appliquées pour calculer l'heure locale à partir de l'heure lue sur un cadran solaire:
1. Correction due à l'heure d'été
2. Correction due au décalage horaire (Longitude)
3. Correction due à l'écart entre le temps solaire moyen et le temps solaire vrai (Équation du temps)